I. Wigner’s theorem
Definition
Let ![]() . The probability distribution on
. The probability distribution on ![]() defined by
defined by
![]()
is called the semi-circular distribution. We denote
Wigner’s Theorem
– Let ![]() i.i.d. centered, complex valued and with
i.i.d. centered, complex valued and with ![]() .
.
– Let ![]() i.i.d. centered, real valued with
i.i.d. centered, real valued with ![]() .
.
– The ![]() ‘s and the
‘s and the ![]() ‘s (
‘s (![]() ) are independent.
) are independent.
– Consider ![]() and
and ![]() the
the ![]() hermitian matrices defined by
hermitian matrices defined by
![]()
Then almost surely,
![Rendered by QuickLaTeX.com \[L_N = \frac{1}{N} \sum_{i=1}^N \delta_{\lambda_i(Y_N)} \overset{\mathcal D}{\underset{N \to \infty}{\longrightarrow }} \mathbb P_{sc,\sigma^2},\]](http://quentin-duchemin.alwaysdata.net/wiki/wp-content/ql-cache/quicklatex.com-d2f0fe5e2959a696de06bd667a2b9159_l3.png)
where
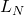 (in cyan) for different values of
(in cyan) for different values of 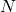 .
. Proof
- Show that semi circular law is characterized by its moments (using a corollary of Carleman theorem). Compute the moments of the smi-circular law (and find the Catalan numbers).
- Compute the moments of the spectral density of the Wigner matrix.
- Show that the moments convergences to the Catalan numbers.
- Convergence of moments + limit distribution characterized by moments -> weak convergence
Additional results
- If
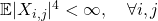 , then
, then ![Rendered by QuickLaTeX.com \[\lambda_{\max}(Y_N) \overset{a.s.}{\underset{N \to \infty}{\to}} 2 \sigma^2 \quad \text{and} \quad \lambda_{\min}(Y_N) \overset{a.s.}{\underset{N \to \infty}{\to}} -2 \sigma^2.\]](http://quentin-duchemin.alwaysdata.net/wiki/wp-content/ql-cache/quicklatex.com-5b0523013263b9684c8aa96748d09f43_l3.png)
In particular,![Rendered by QuickLaTeX.com \[\|Y_N\| = \max\left( |\lambda_{\max}(Y_N)| \; , \; |\lambda_{\min}(Y_N)| \right) \overset{a.s.}{\underset{N \to \infty}{\to}} 2\sigma^2.\]](http://quentin-duchemin.alwaysdata.net/wiki/wp-content/ql-cache/quicklatex.com-0be856b379689cac93289bedf17276c7_l3.png)
- If
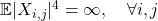 , then
, then ![Rendered by QuickLaTeX.com \[\lambda_{\max}(Y_N) \overset{a.s.}{\underset{N \to \infty}{\to}} + \infty.\]](http://quentin-duchemin.alwaysdata.net/wiki/wp-content/ql-cache/quicklatex.com-7b8aebca2157fe3c636ac743e79b7f54_l3.png)
Remark.
We refer to the paper “The eigenvalues of random symmetric matrices” to get an extension of the Wigner’s Theorem.
II. Marcenko pastur
1. Preliminaries
a) Key results for the proof of the Marcenko-Pastur Theorem
Definition
Let us consider ![]() a probability measure on
a probability measure on ![]() . The Stieltjes transform of
. The Stieltjes transform of ![]() denoted
denoted ![]() is defined by
is defined by
![]()
Theorem (Properties of the Stieltjes Transform)
Let ![]() be some measure on
be some measure on ![]() with Stieltjes Transform
with Stieltjes Transform ![]() .
.
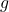 is analytic on
is analytic on 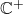 .
.
- If Supp(
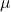 )
) 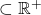 , then
, then 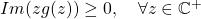 .
. 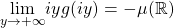 .
.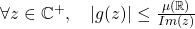 .
.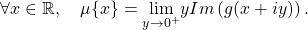
- For any
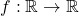 is bounded and continuous,
is bounded and continuous, ![Rendered by QuickLaTeX.com \[\int f d\mu = \underset{y\to 0^+}{\lim} \frac{1}{\pi} \int f(x) Im\left( g(x+iy) \right)dx.\]](http://quentin-duchemin.alwaysdata.net/wiki/wp-content/ql-cache/quicklatex.com-a9f85d32bb5a9be7eccc397ba78825f8_l3.png)
- For all
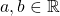 points of continuity of
points of continuity of 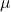 ,
, ![Rendered by QuickLaTeX.com \[ \mu \; (a,b)=\underset{y\to 0^+}{\lim} \frac{1}{\pi} \int_a^b g(x+iy)dx. \]](http://quentin-duchemin.alwaysdata.net/wiki/wp-content/ql-cache/quicklatex.com-6e55c17cc7e43bce1704118c4960f435_l3.png)
Remark. The previous Theorem states that the Stieltjes Transform is analytic on ![]() and when
and when ![]() goes to the real axis, the holomorph property is lost but this allows to recover the measure
goes to the real axis, the holomorph property is lost but this allows to recover the measure ![]() (see properties 6, 7 and 8).
(see properties 6, 7 and 8).
Theorem (Weak convergence and pointwise convergence of Stieltjes Transform)
Let us consider ![]() probability measures on
probability measures on ![]() .
.
- If
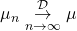 , then
, then ![Rendered by QuickLaTeX.com \[\forall z \in \mathbb C^+, \quad g_{\mu_n}(z) \underset{n \to \infty}{\to} g_{\mu}(z).\]](http://quentin-duchemin.alwaysdata.net/wiki/wp-content/ql-cache/quicklatex.com-38ff5cba35171c5eca474f6b74a6cd35_l3.png)
- a) Let us consider
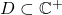 with an accumulation point. If
with an accumulation point. If 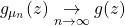 for all
for all 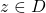 , then
, then
– there exists a measure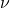 satisfying
satisfying 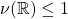 such that
such that ![Rendered by QuickLaTeX.com \[ g(z)= \int \frac{\nu(d\lambda)}{\lambda -z}, \quad \forall z \in \mathbb C^+.\]](http://quentin-duchemin.alwaysdata.net/wiki/wp-content/ql-cache/quicklatex.com-32779992a1ae8ecb8e60aaddf4f19c17_l3.png)
–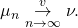
b) If it also holds that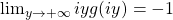 (i.e.
(i.e. 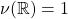 from point 4) of the previous Theorem), then
from point 4) of the previous Theorem), then 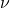 is a probability measure and
is a probability measure and 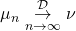 .
.
The previous Theorem can be seen as the counterpart of the famous Levy Theorem. The Levy Theorem states the link between the weak convergence and the pointwise convergence of the characteristic function.
Definition
The characteristic function of a real-valued random variable ![]() is defined by
is defined by
![]()
Theorem (Levy)
Let us consider real-valued random variables ![]() and
and ![]() .
.
- If
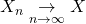 , then
, then 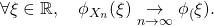
- If there exists some function
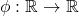 such that
such that
and if![Rendered by QuickLaTeX.com \[ \phi_{X_n}(\xi)\underset{n \to \infty}{\to}\phi(\xi), \quad \forall \xi \in \mathbb R,\]](http://quentin-duchemin.alwaysdata.net/wiki/wp-content/ql-cache/quicklatex.com-b44ecd273677e758b393c7b057500c25_l3.png)
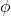 is continuous at
is continuous at 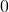 , then
, then
– there exists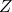 a real valued random variable such that
a real valued random variable such that 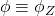 .
.
–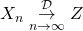 .
.
Just for the sake of beauty, let me mention the following result that can allow to identify functions that can be written as the Stieltjes Transform of some measure ![]() on
on ![]() .
.
Theorem (Recognize a Stieltjes Transform)
If ![]() satisfies
satisfies
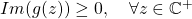
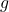 is analytic
is analytic- There exists
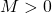 such that
such that 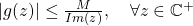
Then there exists a unique measure ![]() on
on ![]() satisfying
satisfying ![]() such that
such that ![]()
If additionally it holds
4. ![]() ,
,
Then ![]() .
.
Example: If ![]() is the Stieltjes Transform of some measure
is the Stieltjes Transform of some measure ![]() then
then ![]() is the Stieltjes Transform of some probability measure
is the Stieltjes Transform of some probability measure ![]() on
on ![]() .
.
b) Proof of the key preliminary result
We will need the following additional properties in the proof.
Theorem (Helly’s selection theorem)
From every sequence of proba measures ![]() , one can extract a subsequence that converges vaguely to a measure
, one can extract a subsequence that converges vaguely to a measure ![]() . (Note that
. (Note that ![]() is not necessary a probability measure).
is not necessary a probability measure).
Remark. ![]() vaguely implies
vaguely implies ![]() for every
for every ![]() where
where
![]()
Proof.
1) To prove that for any ![]() ,
, ![]() , we show that for any
, we show that for any ![]() ,
, ![]() and
and ![]() . Let us consider some
. Let us consider some ![]() . Since
. Since
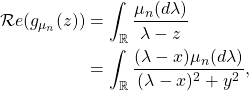
and since
![]()
Using an analogous approach, one can show that
![]()
2a) We consider some set ![]() with an accumulation point such that
with an accumulation point such that ![]() .
.
By the Helly’s selection Theorem, there exists a subsequence ![]() of the sequence of probabilities
of the sequence of probabilities ![]() that converges vaguely to some measure
that converges vaguely to some measure ![]() on
on ![]() . Let us consider some
. Let us consider some ![]() . Using the previous remark and since
. Using the previous remark and since ![]() belongs to
belongs to ![]() , we get that
, we get that
![]()
Since
(1) ![]()
We know from the properties of the Stieltjes Transform that
![]()
We also get that
![]()
Using again the analytic continuation, we obtain that
![]()
leading to
![]()
2b) This directly follows from the equivalece between points ![]() and
and ![]() of the following Lemma.
of the following Lemma.
Lemma
Let ![]() be probability measures and
be probability measures and ![]() be a measure on
be a measure on ![]() . The following statements are equivalent.
. The following statements are equivalent.![]()
![]() .
.![]()
![]() and
and ![]() .
. ![]()
![]() and
and ![]() is tight, namely for any
is tight, namely for any ![]() , there exists some compact set
, there exists some compact set ![]() such that
such that
![]()
2. Marcenko-Pastur Theorem
Theorem (Marcenko-Pastur)
Let us consider a ![]() matrix
matrix ![]() with i.i.d. entries such that
with i.i.d. entries such that ![]()
with ![]() and
and ![]() of the same order and
of the same order and ![]() the spectral measure of
the spectral measure of ![]() :
:![Rendered by QuickLaTeX.com \[c_n = \frac{N}{n} \underset{n \to \infty}{\to} c \in (0,\infty), \quad L_N = \frac{1}{N} \sum_{i=1}^N \delta_{\lambda_i}, \quad \lambda_i=\lambda_i \left(\frac{1}{n} X_N X_N^*\right).\]](http://quentin-duchemin.alwaysdata.net/wiki/wp-content/ql-cache/quicklatex.com-46ff948ffd55b8efbf4fbea192d11b8f_l3.png)
Then, almost surely (i.e. for almost every realization), ![]()
where ![]() is the Marcenko-Pastur distribution
is the Marcenko-Pastur distribution![Rendered by QuickLaTeX.com \[\mathbb P_{MP}(dx)=\left(1-\frac{1}{c}\right)_+ \delta_0 + \frac{\sqrt{\left[ (\lambda^+-x)(x-\lambda^-)\right]_+}}{2\pi\sigma^2xc}dx,\]](http://quentin-duchemin.alwaysdata.net/wiki/wp-content/ql-cache/quicklatex.com-a05d745d915829d2d48f3f48021f1a1b_l3.png)
with![]()
In what follows, we denote ![]() the Stieltjes Transform of the measure
the Stieltjes Transform of the measure ![]() .
.
Remark
- The behavior of the spectral measure brings information about the vast majority of the eigenvalues but is not affected by some individual eigenvalues’ behavior. For example, one may have
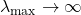 without affecting the behaviour of the whole sum.
without affecting the behaviour of the whole sum. - The Dirac measure at zero is an artifact due to the dimensions of the matrix if
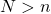 .
. - If
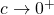 , that is
, that is 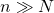 , then typical from the usual regime “small dimensional data vs large samples”. The support of Marcenko-Pastur distribution
, then typical from the usual regime “small dimensional data vs large samples”. The support of Marcenko-Pastur distribution ![Rendered by QuickLaTeX.com [\sigma^2 (1-\sqrt{c})^2, \sigma^2 (1+\sqrt{c})^2]](http://quentin-duchemin.alwaysdata.net/wiki/wp-content/ql-cache/quicklatex.com-d31be14cd518b9792025ed1b59f72cf5_l3.png) concentrates around
concentrates around 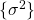 and
and ![Rendered by QuickLaTeX.com \[\mathbb P_{MP} \underset{c\to 0}{\to}\delta_{\sigma^2}.\]](http://quentin-duchemin.alwaysdata.net/wiki/wp-content/ql-cache/quicklatex.com-64e398a189d876fa0efe37f148cd058c_l3.png)
(2) ![]()
This will allow to show that there exists some set
![]()
Indeed, suppose that we know that (2) holds et let us consider some sequence
(3) ![]()
holds for any
![]()
(note that we used the continuity of the functions
We will then conclude the proof of the Theorem using the Theorem of the previous section (called Weak convergence and pointwise convergence of Stieltjes Transform).
To prove (2), we use the decomposition
![]()
- To deal with the term
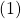 , we use the Efron-Stein inequality to show that
, we use the Efron-Stein inequality to show that ![Rendered by QuickLaTeX.com \[Var(g_n(z)) = \mathcal O\left(\frac{1}{n^2}\right), \]](http://quentin-duchemin.alwaysdata.net/wiki/wp-content/ql-cache/quicklatex.com-ed6b88a01aa1dd5442cd60640b46391d_l3.png)
which allows to prove that almost surely![Rendered by QuickLaTeX.com g_n(z) - \mathbb E [ g_n(z)]](http://quentin-duchemin.alwaysdata.net/wiki/wp-content/ql-cache/quicklatex.com-f0f42caf9e972ec048dbeab8c7f3a7c3_l3.png) tends to
tends to 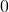 using Borel-Cantelli Lemma.
using Borel-Cantelli Lemma. - We then show that
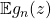 satisfies
satisfies (4)
and that![Rendered by QuickLaTeX.com \begin{equation*} z \sigma^2 c_n \left( \mathbb E g_n(z) \right)^2+ \left[ z + \sigma^2(c_n-1)\right] \mathbb E g_n(z)+1 = \mathcal O_z(n^{1/2}),\end{equation*}](http://quentin-duchemin.alwaysdata.net/wiki/wp-content/ql-cache/quicklatex.com-1f1d491745b2775153b4defddcaba3ba_l3.png)
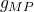 satisfies the equation
satisfies the equation(5)
![Rendered by QuickLaTeX.com \begin{equation*} z \sigma^2 c \left( \mathbb E g_{MP}(z) \right)^2+ \left[ z + \sigma^2(c-1)\right] \mathbb E g_{MP}(z)+1 =0. \end{equation*}](http://quentin-duchemin.alwaysdata.net/wiki/wp-content/ql-cache/quicklatex.com-424118d0b7cdf6ec42fcd3d778096c6e_l3.png)
- To conclude the proof (i.e. to get (2)), we use some “stability” result. More precisely, equations (4) and (5) are close and we need to show that solutions of these equations are as a consequence, close to each other. We formalize this result with the following Lemma.
Lemma
Let ![]() . We assume that there exists two Stieltjes Transform of probability measures on
. We assume that there exists two Stieltjes Transform of probability measures on ![]() , denoted
, denoted ![]() , that are respectively the solutions of the equation
, that are respectively the solutions of the equation
![Rendered by QuickLaTeX.com \begin{align*}z \sigma^2 c X^2+ \left[ z + \sigma^2(c-1)\right]X+1 &=0 \\z \sigma^2 c_{\delta} X_{\delta}^2+ \left[ z + \sigma^2(c_{\delta}-1)\right]X_{\delta}+1 &=0 ,\end{align*}](http://quentin-duchemin.alwaysdata.net/wiki/wp-content/ql-cache/quicklatex.com-5695ce0298dce6780fbd569209e03448_l3.png)
where
![]()
Let
![]()
and
![]()
Theorem (convergence of extremal eigenvalues)
- If
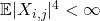 , then
, then ![Rendered by QuickLaTeX.com \[\lambda_{\max} \overset{a.s.}{\underset{N,n \to \infty}{\to}} \sigma^2(1+\sqrt{c})^2 \quad \text{and} \quad \lambda_{\min} \overset{a.s.}{\underset{N,n \to \infty}{\to}} \sigma^2(1-\sqrt{c})^2.\]](http://quentin-duchemin.alwaysdata.net/wiki/wp-content/ql-cache/quicklatex.com-16e9b86fcabc2cb039ecc399f71fde14_l3.png)
- If
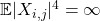 , then
, then ![Rendered by QuickLaTeX.com \[\lambda_{\max} \overset{a.s.}{\underset{N,n \to \infty}{\to}} +\infty \quad \text{and} \quad \lambda_{\min} \overset{a.s.}{\underset{N,n \to \infty}{\to}} \sigma^2(1-\sqrt{c})^2.\]](http://quentin-duchemin.alwaysdata.net/wiki/wp-content/ql-cache/quicklatex.com-065804977c836ce9ccc584b9dcd7b5e1_l3.png)
Remark.
Exactly like with Wigner matrices, when the 4th moment of the random varaibles ![]() are not finite,
are not finite, ![]() goes to
goes to ![]() . However, contrary to the Wigner case, for Wishart matrices
. However, contrary to the Wigner case, for Wishart matrices ![]() still converges to a finite value.
still converges to a finite value.
Theorem (Fluctuations of ![]() and Tracy-Widom distribution)
and Tracy-Widom distribution)
We can fully describe the fluctuations of ![]() :
:
![]()
where
![]()
