In many situations, there is a symmetric matrix of interest ![]() , but one only has a perturbed version of it
, but one only has a perturbed version of it ![]() . How is
. How is ![]() affected by
affected by ![]() ?
?
The basic example is Principal Component Analysis (PCA). Let ![]() for some random vector
for some random vector ![]() , and let
, and let ![]() be the sample covariance matrix on independent copies of
be the sample covariance matrix on independent copies of ![]() . Namely, we observe
. Namely, we observe ![]() i.i.d. random variable distributed as
i.i.d. random variable distributed as ![]() and we set
and we set
![]()
1. Some intuition
An eigenspace of ![]() is the span of some eigenvectors of
is the span of some eigenvectors of ![]() . We can decompose
. We can decompose ![]() into its action on an eigenspace
into its action on an eigenspace ![]() and its action on the orthogonal complement
and its action on the orthogonal complement ![]() :
:
![]()
where
![]()
Suppose we find a few eigenvalues of
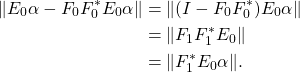
Therefore vectors in ![]() will be well-approximated by
will be well-approximated by ![]() if
if ![]() is “small”.
is “small”.
The condition we will need is separation between the eigenvalues corresponding to ![]() and those corresponding to
and those corresponding to ![]() . Suppose the eigenvalues corresponding to
. Suppose the eigenvalues corresponding to ![]() are all contained in an interval
are all contained in an interval ![]() . Then we will require that the eigenvalues corresponding to
. Then we will require that the eigenvalues corresponding to ![]() be excluded from the interval
be excluded from the interval ![]() for some
for some ![]() . To see why this is necessary, consider the following example:
. To see why this is necessary, consider the following example:
![]()
Here, the “size” of
arbitrarily large relative to
2. Distances between subspaces
Let ![]() and
and ![]() be
be ![]() -dimensional subspaces of
-dimensional subspaces of ![]() , with
, with ![]() . Let
. Let ![]() and
and ![]() be projectors onto these two subspaces.
be projectors onto these two subspaces.
We first consider the angle between two vectors, that is, when ![]() . Then,
. Then, ![]() and
and ![]() are spanned by vectors. Denote the two corresponding vectors as
are spanned by vectors. Denote the two corresponding vectors as ![]() . The angle between
. The angle between ![]() and
and ![]() is defined as:
is defined as:
![]()
Now, we need to extend this concept to subspaces (when
Now, we define the angle between subspaces
Definition
The canonical or principal angles between ![]() and
and ![]() are:
are:
![]()
where
A general result known as CS-decomposition in linear algebra gives the following:
![]()
where
![Rendered by QuickLaTeX.com \[\Theta = \begin{bmatrix} \theta_1 & \dots & 0 \\ \vdots & \dots & \vdots \\ 0 & \dots & \theta_r \end{bmatrix}\]](https://quentin-duchemin.alwaysdata.net/wiki/wp-content/ql-cache/quicklatex.com-f9385e6988084442cc05f07f7052e2e3_l3.png)
Another way of defining canonical angles is the following:
Definition
The canonical angles between the spaces ![]() and
and ![]() are
are ![]() for
for ![]() , where
, where ![]() are the singular values of
are the singular values of
![]()
Now, given the definition of the canonical angles, we can define the distances between subspaces ![]() and
and ![]() as the following.
as the following.
Definition
The distance between ![]() and
and ![]() is
is ![]() , which is a metric over the space of
, which is a metric over the space of ![]() -dimensional linear subspaces of
-dimensional linear subspaces of ![]() . Equivalently,
. Equivalently,
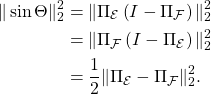
3. Davis Kahan Theorem
Theorem
Let ![]() and
and ![]() be symmetric matrices with
be symmetric matrices with ![]() and
and ![]() orthogonal matrices. If the eigenvalues
orthogonal matrices. If the eigenvalues ![]() are contained in an interval
are contained in an interval ![]() , and the eigenvalues of
, and the eigenvalues of ![]() are excluded from the interval
are excluded from the interval ![]() for some
for some ![]() , then
, then
![]()
for any unitarily invariant norm
Proof.
Since ![]() we have
we have
![]()
Furthermore,
![]()
Let
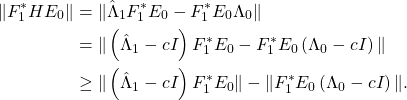
Here we have used a centering trick so that
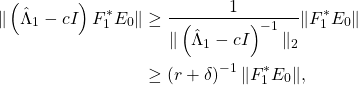
and
![]()
We conclude that
Another version of the Davis-Kahan Theorem which is more popular in the community of statisticians is the following.
Theorem
Let ![]() and
and ![]() be
be ![]() symmetric matrices with respective eigenvalues
symmetric matrices with respective eigenvalues ![]() and
and ![]() .
.
Fix ![]() , and let
, and let ![]() and
and ![]() be
be ![]() matrices with orthonormal columns corresponding to eigenvalues
matrices with orthonormal columns corresponding to eigenvalues ![]() and
and ![]() .
.
Let ![]() and
and ![]() be the subspaces spanned by columns of
be the subspaces spanned by columns of ![]() and
and ![]() . Define the eigengap as
. Define the eigengap as
![]()
where we define
If
![]()
The result also holds for the operator norm
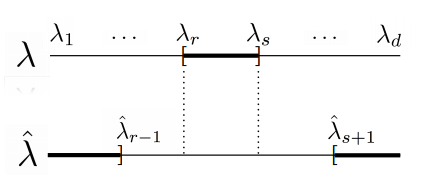
 . (Source: Alessandro Rinaldo Lecture Notes)
. (Source: Alessandro Rinaldo Lecture Notes)By Weyl’s theorem, one can show that the sufficient (but not necessary) condition for ![]() in Davis-Kahan theorem is
in Davis-Kahan theorem is
![]()
When the matrices are not symmetric, there exists a generalized version of the Davis-Kahan Theorem called Wedin’s theorem.
