Slepian and Gordon Theorems with application

In this post, we present two important results of the field of Gaussian Processes: the Slepian and Gordon Theorems. For both of them, we illustrate their power giving specific applications to random matrix theory. More precisely, we derive bounds on the expected operator norm of gaussian matrices.

1. Slepian’s Theorem and application

Theorem (Slepian Fernique 71′)
Let $X=(X_1, \dots,X_n)$ and $Y=(Y_1,\dots,Y_n)$ be two centered gaussian vectors such that

$\forall i,j \quad \mathbb E |X_i-X_j|^2 \leq \mathbb E |Y_i-Y_j|^2.$

Then,

$\mathbb E \sup_{1\leq i \leq n}X_i \leq \mathbb E\sup_{1\leq i \leq n} Y_i.$

Theorem (Slepian 65′)
We keep assumptions and notations of the Slepian-Fernique Theorem and we ask further that

$\forall i , \quad \mathbb E X_i^2=\mathbb E Y_i^2.$

Then it holds

$\forall t \in \mathbb R, \quad \mathbb P\left( \sup_{1\leq i \leq n} X_i \geq t \right) \leq \mathbb P \left( \sup_{1\leq i \leq n} Y_i \geq t \right).$

Remarks:
$\bullet$ The assumptions of the Slepian’s Theorem, namely $\mathbb E X_i^2 = \mathbb E Y_i^2$ and $\mathbb E |X_i-X_j|^2 \leq \mathbb E |Y_i-Y_j|^2$ are equivalent to the following condition

$\Sigma_X \geq \Sigma_Y \text{ with same diagonals.}$

Stated otherwise, the covariance matrices $\Sigma_X$ and $\Sigma_Y$ of $X$ and $Y$ are entrywise comparable with the coefficient of $\Sigma_X$ greater or equal to those of $\Sigma_Y$ with the same variances.
$\bullet$ Note that since

$\mathbb E \sup_i \; X_i = \int_{-\infty}^{+\infty} \mathbb P\left( \sup_i X_i \geq t \right)dt,$

the conclusion of the Slepian’s Theorem is stronger compared to the one of the Slepian-Fernique’s Theorem.

Consequence

$(i)$ Let us consider $G=(g_{i,j})_{1\leq i \leq n, \; 1\leq j \leq m}$ a random variable variables taking values in $\mathbb R^{n\times m}$ with entries $g_{i,j}\sim \mathcal N(0,1)$ . Then, denoting $\|\cdot \|$ the operator norm, it holds

$\mathbb E \|G\| \leq \mathbb E\left( \sum_{i=1}^n g_i^2 \right)^{1/2}+\mathbb E\left( \sum_{j=1}^m h_j^2 \right)^{1/2} \leq \sqrt{n}+\sqrt{m},$

where for all $i \in [n],$ $g_i \sim \mathcal N(0,1)$ and for all $j \in [n],$ $h_j \sim \mathcal N(0,1)$ .
$(ii)$ Moreover, $\forall t >0,$

$\mathbb P\left( \|G\|\geq \sqrt{m}+\sqrt{n}+t\right)\leq e^{-\frac{t^2}{2}},$

i.e.

$\forall \epsilon>0, \quad \mathbb P \left( \|G\|\geq (1+\epsilon)(\sqrt{n}+\sqrt{m} )\right) \leq e^{-\epsilon^2(k+n)}.$

Proof.

Let us recall that

$\|G\|=\sup_{x \in \mathbb S^{m-1}} \|Gx\|_2 = \sup_{x \in \mathbb S^{m-1}}\sup_{y \in \mathbb S^{n-1}} \langle Gx,y \rangle.$

Hence it holds

$\mathbb E \|G\|= \mathbb E \left[ \sup_{x \in \mathbb S^{m-1}}\sup_{y \in \mathbb S^{n-1}} X_{x,y} \right],$

where for all $(x,y) \in \mathbb S^{m-1}\times \mathbb S^{n-1}$ , $X_{x,y} = \sum_{i=1}^n \sum_{j=1}^m g_{i,j} x_j y_i \sim \mathcal N(0,1).$

Let us first consider finite sets $S \subset \mathbb S^{m-1}$ and $T \subset \mathbb S^{n-1}$ . Then we get for any $x,\overline{x} \in S$ and any $y, \overline{y} \in T$ ,

$\begin{align*}\mathbb E |X_{x,y}-X_{\overline{x},\overline{y}}|^2 &= \mathbb E \left|\sum_{i=1}^m \sum_{j=1}^n g_{i,j}(x_jy_i-\overline{x}_j\overline{y}_i)\right|^2\\&= \sum_{i=1}^m \sum_{j=1}^n (x_jy_i-\overline{x}_j\overline{y}_i)^2\\&= 2\left( 1 - \sum_{i=1}^m \sum_{j=1}^n x_jy_i\overline{x}_j \overline{y}_i\right)\\&= 2\left( 1 -\langle x , y \rangle \langle \overline{x},\overline{y}\rangle \right)\\&=\|x-\overline{x}\|^2_2 + \langle x,\overline{x} \rangle \|y-\overline{y}\|^2_2,\end{align*}$

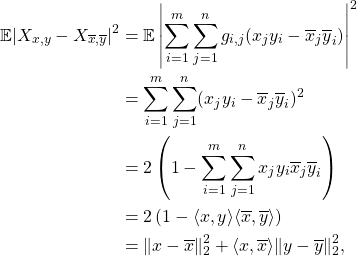
where in the last equality, we used the fact that $x,y,\overline{x}$ and $\overline{y}$ have a $l_2$ -norm equal to $1$ . Hence we proved that $\forall (x,y)\in S\times T,$ $\forall (\overline{x}, \overline{y}) \in S \times T$ ,

$\mathbb E \left| X_{x,y} - X_{\overline{x},\overline{y}\right|^2 \leq \|x-\overline{x}\|^2 + \|y-\overline{y}\|^2_2.$

Now, let us introduce for any $(x,y)\in S\times T$ the random variable

$Y_{x,y} = \sum_{i=1}^n y_i g_i + \sum_{j=1}^m x_j h_j,$

with $g_i,h_j \overset{i.i.d.}{\sim} \mathcal N(0,1)$ . Then,

$\mathbb E \left| Y_{x,y} - Y_{\overline{x},\overline{y}} \right|^2 =\|x-\overline{x}\|_2^2+\|y-\overline{y}\|_2^2,$

leading to

$\forall (x,y)\in S\times T,$ $\forall (\overline{x}, \overline{y}) \in S \times T, \quad \mathbb E \left| X_{x,y} - X_{\overline{x},\overline{y}} \right|^2 \leq \mathbb E \left| Y_{x,y} - Y_{\overline{x},\overline{y}} \right|^2.$

We can then apply the Slepian Fernique theorem to obtain that

$\begin{align*}\mathbb E \left(\underset{x \in S}{\sup} \; \underset{y \in T}{\sup} X_{x,y} \right) &\leq \mathbb E \left(\underset{x \in S}{\sup} \; \underset{y \in T}{\sup} Y_{x,y} \right) \\&= \mathbb E \left(\underset{x \in S}{\sup} \sum_{i=1}^n y_i g_i + \underset{y \in T}{\sup} \sum_{j=1}^m x_j h_j \right) \\&= \mathbb E \left[ \left(\sum_{i=1}^n y_i^2 \right)^{1/2}+ \left(\sum_{j=1}^m x_j^2 \right)^{1/2}\right] \\&\leq \left( \mathbb E \left[\sum_{i=1}^n y_i^2 \right]\right)^{1/2}+ \left(\mathbb E \left[\sum_{j=1}^m x_j^2 \right] \right)^{1/2} \\&= \sqrt{m} + \sqrt{n}.\end{align*}$

To conclude the proof, we need to show that the previous computations derived with finite sets $S$ and $T$ are enough to get a bound on the operator norm (for which the supremum run on both $\mathbb S^{m-1}$ and $\mathbb S^{n-1}$ ). For this, we need to introduce the notion of covering sets.

Definition
Let us consider $n \in \mathbb N^*$ and $\epsilon >0$ . A set $S \subset \mathbb S^{n-1}$ is called an $\epsilon$ -net (covering) of $\mathbb S^{n-1}$ , if

$\forall u \in \mathbb S^{n-1}, \quad \exists v \in S \quad \text{ s.t.}\quad \|u-v\|_2 \leq \epsilon.$

Then, the following Lemma proves that it is sufficient to work with supremum on finite sets rather than the whole continuous spaces $\mathbb S^{n-1}$ and $\mathbb S^{m-1}$ . By taking the limit $\epsilon \to 0$ , the Lemma and the previous computations directly give the stated bound for the expected operator norm of a gaussian matrix $G$ .

Lemma
$i)$ There exists an $\epsilon$ -net $S$ for $\mathbb S^{n-1}$ of size $|S | \leq \left(1 + \frac{2}{\epsilon} \right)^n.$
$ii)$ For $S$ an $\epsilon$ -net,

$\max_{v \in S} |v^{\top}Gv|\leq \|G\| \leq \frac{1}{1-2\epsilon} \max_{v \in S} |v^{\top}Gv|.$

2. Gordon’s Theorem and application

Gordon’s Theorem
Let $X=(X_{i,j})$ and $Y=(Y_{i,j})$ be two centered gaussian processes such that

$\mathbb E (X_{i,j}-X_{i,k})^2 \geq \mathbb E (Y_{i,j}-Y_{i,k})^2, \quad \forall i,j,k$

$\mathbb E (X_{i,j}-X_{i',j'})^2 \leq \mathbb E (Y_{i,j}-Y_{i',j'})^2, \quad \forall i\neq i', \; \forall j,j'.$

Then

$\mathbb E \inf_i \sup_j X_{i,j} \geq \mathbb E \inf_i \sup_j Y_{i,j}.$

Remarks
If we apply Gordon’s inequality for $-X_{i,j}$ and $-Y_{i,j}$ , we get $\mathbb E \sup_{i} \inf_j X_{i,j} \leq \mathbb E \sup_i \inf_j Y_{i,j}$ . Hence Gordon’s inequality contains Slepian’s inequality by taking the second index set to be a singleton set.

Consequence

For a given matrix $A \in \mathbb R^{n\times m}$ , if $\mathrm{Ker}(A)=\{0\}$ (meaning that the linear map $x \mapsto Ax$ is injective), then the map

$\begin{align*}\mathbb R^m &\to \mathrm{Im}(A) \\ x & \mapsto Ax\end{align*}$

is an isomorphism with inverse denoted $A^{-1}$ . The operator norm of $A^{-1}$ is given by

$\begin{align*}\|A^{-1}\| &= \underset{y \in Im(A) \backslash \{0\}}{\sup} \frac{\|A^{-1}y\|_2}{\|y\|_2} = \underset{x \in \mathbb R^m \backslash \{0\}}{\sup} \frac{\|x\|_2}{\|Ax\|_2}\\&=\left( \underset{x \in \mathbb S^{m-1}}{\inf } \|Ax\|_2\right)^{-1}=\left( \underset{x \in \mathbb S^{m-1}}{\inf } \underset{y \in \mathbb S^{n-1}}{\sup} \langle Ax,y \rangle \right)^{-1}.\end{align*}$

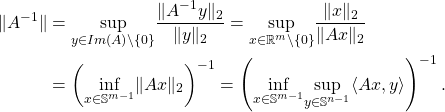
Hence, the previous expression allows us to understand that the Gordon Theorem can be a convenient tool to upper bound the expected value of the inverse of the operator norm of the inverse of a gaussian matrix $G$ . Following an approach similar to the previous section, one can prove that

$\mathbb E \|G\| \; \times \; \mathbb E \frac{1}{\|G^{-1}\|}\leq \frac{1+\epsilon}{1-\epsilon},$

with

$\epsilon = \frac{\mathbb E \left( \sum_{j=1}^m h_j^2 \right)^{1/2}}{\mathbb E \left( \sum_{i=1}^n g_i^2 \right)^{1/2}}.$

Remark
Let us finally point out that the approaches used in the proofs can allow to get a uniform bound for a random quadratic form given by

$\sup_{x \in S, \; y \in T} \langle Ax,y \rangle,$

where $S \subset \mathbb R^{m}$ and $T \subset \mathbb R^n$ are arbitrary bounded sets. Such inequality can be given by the Chevet’s inequality which states that given a $m \times n$ matrix $A$ whose entries $A_{ij}$ are independent, mean zero, sub-gaussian random variables, it holds

$\mathbb E \sup_{ x\in S, \; y \in T} \langle Ax, y\rangle \leq CK \left[ \omega(S)\mathrm{rad}(T) + \omega(T) \mathrm{rad}(S)\right] ,$

where $C>0$ is an absolute constant and where $K:= \max_{i,j} \|A_{i,j}\|_{\psi_2}$ is the maximum of the 2-Orlicz norms of the entries of $A$ . $\omega(T)$ and $\mathrm{rad}(T)$ are respectively the gaussian width and the radius of the set $T$ and are defined as follows

$\omega(T) := \mathbb E \sup_{t\in T} \langle t, Z \rangle \quad \text{ and } \quad \mathrm{rad}(T):= \sup_{t \in T} \|t\|_2 ,$