In this post, we present two important results of the field of Gaussian Processes: the Slepian and Gordon Theorems. For both of them, we illustrate their power giving specific applications to random matrix theory. More precisely, we derive bounds on the expected operator norm of gaussian matrices.
1. Slepian’s Theorem and application
Theorem (Slepian Fernique 71′)
Let ![]() and
and ![]() be two centered gaussian vectors such that
be two centered gaussian vectors such that
![]()
Then,
![]()
Theorem (Slepian 65′)
We keep assumptions and notations of the Slepian-Fernique Theorem and we ask further that
![]()
Then it holds
![]()
Remarks:![]() The assumptions of the Slepian’s Theorem, namely
The assumptions of the Slepian’s Theorem, namely ![]() and
and ![]() are equivalent to the following condition
are equivalent to the following condition
![]()
Stated otherwise, the covariance matrices
![]()
Consequence
![]() Let us consider
Let us consider ![]() a random variable variables taking values in
a random variable variables taking values in ![]() with entries
with entries ![]() . Then, denoting
. Then, denoting ![]() the operator norm, it holds
the operator norm, it holds
![Rendered by QuickLaTeX.com \[\mathbb E \|G\| \leq \mathbb E\left( \sum_{i=1}^n g_i^2 \right)^{1/2}+\mathbb E\left( \sum_{j=1}^m h_j^2 \right)^{1/2} \leq \sqrt{n}+\sqrt{m},\]](https://quentin-duchemin.alwaysdata.net/wiki/wp-content/ql-cache/quicklatex.com-c1788ec43af31283c953a9bb626214d3_l3.png)
where for all
![]()
i.e.
![]()
Proof.
Let us recall that
![]()
Hence it holds
![Rendered by QuickLaTeX.com \[\mathbb E \|G\|= \mathbb E \left[ \sup_{x \in \mathbb S^{m-1}}\sup_{y \in \mathbb S^{n-1}} X_{x,y} \right],\]](https://quentin-duchemin.alwaysdata.net/wiki/wp-content/ql-cache/quicklatex.com-415fba91d1e3160e57add4e1162caf0c_l3.png)
where for all
Let us first consider finite sets ![]() and
and ![]() . Then we get for any
. Then we get for any ![]() and any
and any ![]() ,
,
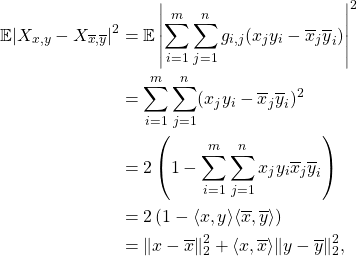
where in the last equality, we used the fact that
![]()
Now, let us introduce for any
![Rendered by QuickLaTeX.com \[Y_{x,y} = \sum_{i=1}^n y_i g_i + \sum_{j=1}^m x_j h_j,\]](https://quentin-duchemin.alwaysdata.net/wiki/wp-content/ql-cache/quicklatex.com-b8ef41d51c8af7838d381ac607f83ff0_l3.png)
with
![]()
leading to
![Rendered by QuickLaTeX.com \[\forall (x,y)\in S\times T,$ $\forall (\overline{x}, \overline{y}) \in S \times T, \quad \mathbb E \left| X_{x,y} - X_{\overline{x},\overline{y}} \right|^2 \leq \mathbb E \left| Y_{x,y} - Y_{\overline{x},\overline{y}} \right|^2.\]](https://quentin-duchemin.alwaysdata.net/wiki/wp-content/ql-cache/quicklatex.com-4e34ba0f98e562890c7d28c099a38293_l3.png)
We can then apply the Slepian Fernique theorem to obtain that
![Rendered by QuickLaTeX.com \begin{align*}\mathbb E \left(\underset{x \in S}{\sup} \; \underset{y \in T}{\sup} X_{x,y} \right) &\leq \mathbb E \left(\underset{x \in S}{\sup} \; \underset{y \in T}{\sup} Y_{x,y} \right) \\&= \mathbb E \left(\underset{x \in S}{\sup} \sum_{i=1}^n y_i g_i + \underset{y \in T}{\sup} \sum_{j=1}^m x_j h_j \right) \\&= \mathbb E \left[ \left(\sum_{i=1}^n y_i^2 \right)^{1/2}+ \left(\sum_{j=1}^m x_j^2 \right)^{1/2}\right] \\&\leq \left( \mathbb E \left[\sum_{i=1}^n y_i^2 \right]\right)^{1/2}+ \left(\mathbb E \left[\sum_{j=1}^m x_j^2 \right] \right)^{1/2} \\&= \sqrt{m} + \sqrt{n}.\end{align*}](https://quentin-duchemin.alwaysdata.net/wiki/wp-content/ql-cache/quicklatex.com-619734f8eeac670cfc0a823f11beb071_l3.png)
To conclude the proof, we need to show that the previous computations derived with finite sets ![]() and
and ![]() are enough to get a bound on the operator norm (for which the supremum run on both
are enough to get a bound on the operator norm (for which the supremum run on both ![]() and
and ![]() ). For this, we need to introduce the notion of covering sets.
). For this, we need to introduce the notion of covering sets.
Definition
Let us consider ![]() and
and ![]() . A set
. A set ![]() is called an
is called an ![]() -net (covering) of
-net (covering) of ![]() , if
, if
![]()
Then, the following Lemma proves that it is sufficient to work with supremum on finite sets rather than the whole continuous spaces ![]() and
and ![]() . By taking the limit
. By taking the limit ![]() , the Lemma and the previous computations directly give the stated bound for the expected operator norm of a gaussian matrix
, the Lemma and the previous computations directly give the stated bound for the expected operator norm of a gaussian matrix ![]() .
.
Lemma![]() There exists an
There exists an ![]() -net
-net ![]() for
for ![]() of size
of size ![]()
![]() For
For ![]() an
an ![]() -net,
-net,
![]()
2. Gordon’s Theorem and application
Gordon’s Theorem
Let ![]() and
and ![]() be two centered gaussian processes such that
be two centered gaussian processes such that
![]()
![]()
Then
![]()
Remarks
If we apply Gordon’s inequality for ![]() and
and ![]() , we get
, we get ![]() . Hence Gordon’s inequality contains Slepian’s inequality by taking the second index set to be a singleton set.
. Hence Gordon’s inequality contains Slepian’s inequality by taking the second index set to be a singleton set.
Consequence
For a given matrix ![]() , if
, if ![]() (meaning that the linear map
(meaning that the linear map ![]() is injective), then the map
is injective), then the map
![]()
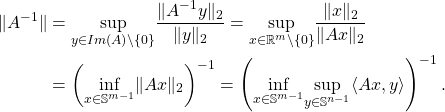
Hence, the previous expression allows us to understand that the Gordon Theorem can be a convenient tool to upper bound the expected value of the inverse of the operator norm of the inverse of a gaussian matrix ![]() . Following an approach similar to the previous section, one can prove that
. Following an approach similar to the previous section, one can prove that
![]()
with
![Rendered by QuickLaTeX.com \[\epsilon = \frac{\mathbb E \left( \sum_{j=1}^m h_j^2 \right)^{1/2}}{\mathbb E \left( \sum_{i=1}^n g_i^2 \right)^{1/2}}.\]](https://quentin-duchemin.alwaysdata.net/wiki/wp-content/ql-cache/quicklatex.com-fb2f7b7d780696be733fc07605524ff5_l3.png)
Remark
Let us finally point out that the approaches used in the proofs can allow to get a uniform bound for a random quadratic form given by
![]()
![]()
![]()
We refer to Section 8.7 of the book High-Dimensional Probability from R.Vershynin for details.
